Maxmizing fuel purchases at the ⛽

Cue references to Superman III and Office Space

May 31, 2017

For the longest time, I would only focus on the cost when putting fuel in my car. However, a quirk in U.S. fuel pricing means I could be shorting the amount of fuel I get for the same cost. Read on to discover the ease of maximizing fuel purchases and why the potential shortage increases with lower fuel prices.

One weird trick...

The idea behind maximizing fuel purchases works by tracking the "hidden" fractional-cost per gallon that is not displayed at the pump. Knowing pumps round-up to the nearest whole-cent at $0.5¢ - 0.9¢$ means needing to figure out what amount of fuel gets us to 0.4¢ past what is spent (displayed at the pump).

If I want to maximize ten-dollars worth of fuel and fuel is $2.459 per gallon, then I need to calculate how much fuel will be pumped at $10.004–which is 4.068 gallons (versus 4.066 gallons at exactly ten-dollars). We can get an extra 0.002 gallons of fuel for the same cost! This is our potential shortage.

Calculation

$("actual money spent" + 0.4¢) / "cost of fuel per gallon" = "maximum amount of fuel based on money spent"$

Maximizing the savings

Since the savings based on the extra 0.4¢ is linear across a single purchase at the pump, we could maximize the savings by essentially making multiple purchases at the lowest-amount ($0.01) where:

$"$0.01 spent" / "$2.459 / gal." = "0.004 gal."$

$"$0.014 spent" / "$2.459 / gal." = "0.006 gal."$

Problems

Of course, this presents a number of problems. Here are a few notables:

It would take a long time to fill-up your vehicle. Assuming a sixteen-gallon tank, it would take 2,667 separate transactions.
Making 2,667 separate transactions via non-cash payment would probably get flagged as suspicious activity.
Owner of the pump would probably wonder why you decided to set up ⛺ at the pump.

Positives

There is the potential to save $12.67, but really?!

Calculation

Spending exactly 1¢ results in a slight overpayment assuming the full sixteen-gallons is purchased, so we'll go with the regular calculation to compare:

$"16 gal." / ("0.004 gal." / "1¢ spent") = 4,000¢\ ($40.00)$

$"16 gal." * (("2,459¢" / "gal.") / "1¢ spent") = 3,934¢\ ($39.34)$

and

$"16 gal." / ("0.006 gal." / "1.4¢ spent") = 2,667¢\ ($26.67)$

Lower prices means more fuel?

There is an inverse relationship between unit of fuel and price per unit of fuel which can be expressed as: $"unit of fuel" = 1 / "cost per unit of fuel"$ or $y = 1 / x$. It looks like this:

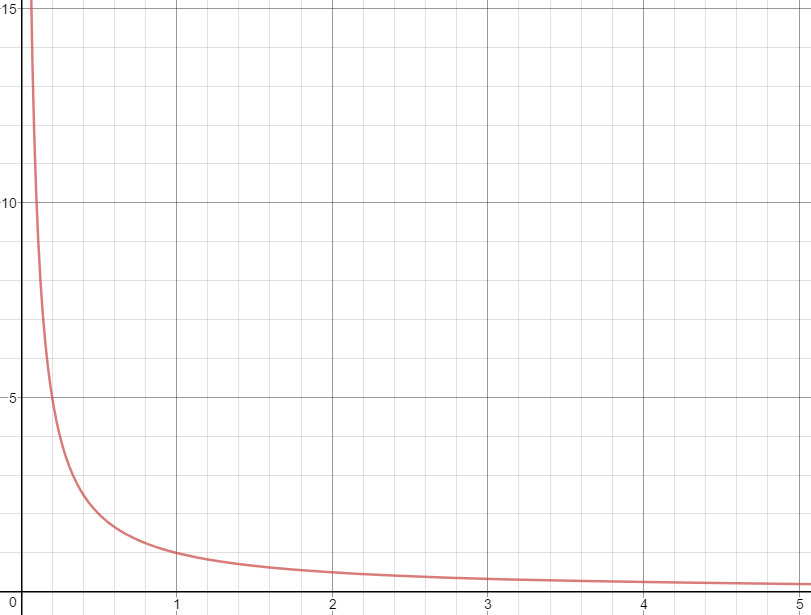
Graph showing relationship between unit of fuel and price per unit of fuel as y = 1 / x

Conclusion

I acknowledge two-thousandths of a gallon is not much. Assuming your vehicle gets thirty miles per gallon, the extra fuel in my example would allow you to potentially travel an extra 316.8 feet. But, maybe there is comfort to knowing if fuel prices never change, after 500 transactions, you will get a free gallon of fuel. Lastly, remember the relationship is inverse, so if price dropped to $"$0.999" / "gal."$, savings would double!

Calculation

$("30 miles" / "1 gal.") * ("5,280 ft." / "1 mile") * "0.002 gal." = "316.8 ft."$

and

$"1 gal." / ("0.002 gal." / "transaction") = "500 transactions"$